How To Draw Proper Free Body Diagrams

Learning Objectives

Past the stop of the section, you will be able to:

• Explain the rules for drawing a free-body diagram
• Construct costless-trunk diagrams for different situations

The first footstep in describing and analyzing most phenomena in physics involves the conscientious cartoon of a free-body diagram. Gratuitous-body diagrams have been used in examples throughout this chapter. Remember that a costless-body diagram must only include the external forces acting on the body of interest. In one case we accept drawn an accurate free-body diagram, we can apply Newton'due south commencement police if the body is in equilibrium (balanced forces; that is, [latex] {F}_{\text{cyberspace}}=0 [/latex]) or Newton's second police force if the body is accelerating (unbalanced force; that is, [latex] {F}_{\text{net}}\ne 0 [/latex]).

In Forces, we gave a brief problem-solving strategy to assist you understand free-body diagrams. Here, we add together some details to the strategy that will help y'all in constructing these diagrams.

Problem-Solving Strategy: Constructing Free-Body Diagrams

Observe the post-obit rules when amalgam a free-body diagram:

1. Describe the object under consideration; it does non have to be creative. At first, you may want to depict a circle around the object of interest to be sure you focus on labeling the forces interim on the object. If you are treating the object as a particle (no size or shape and no rotation), stand for the object as a point. Nosotros oft identify this point at the origin of an xy-coordinate arrangement.
2. Include all forces that act on the object, representing these forces as vectors. Consider the types of forces described in Common Forces—normal force, friction, tension, and jump force—as well as weight and applied forcefulness. Do not include the net force on the object. With the exception of gravity, all of the forces we have discussed require straight contact with the object. However, forces that the object exerts on its surroundings must not be included. Nosotros never include both forces of an action-reaction pair.
3. Convert the free-body diagram into a more detailed diagram showing the x– and y-components of a given forcefulness (this is often helpful when solving a trouble using Newton's outset or 2nd law). In this case, place a squiggly line through the original vector to evidence that it is no longer in play—it has been replaced by its ten– and y-components.
4. If in that location are two or more objects, or bodies, in the problem, draw a separate free-body diagram for each object.

Annotation: If there is acceleration, we practise not straight include it in the free-body diagram; notwithstanding, it may assistance to indicate acceleration exterior the free-body diagram. You can label information technology in a different color to betoken that information technology is separate from the gratis-body diagram.

Let's employ the problem-solving strategy in drawing a free-torso diagram for a sled. In (Figure)(a), a sled is pulled by force P at an angle of [latex] xxx\text{°} [/latex]. In part (b), nosotros bear witness a free-torso diagram for this state of affairs, as described past steps one and ii of the problem-solving strategy. In part (c), we show all forces in terms of their x– and y-components, in keeping with pace 3.

Figure 5.31 (a) A moving sled is shown as (b) a gratis-body diagram and (c) a free-body diagram with force components.

Instance

Two Blocks on an Inclined Plane

Construct the free-body diagram for object A and object B in (Figure).

Strategy

We follow the four steps listed in the problem-solving strategy.

Solution

We offset by creating a diagram for the first object of interest. In (Figure)(a), object A is isolated (circled) and represented by a dot.

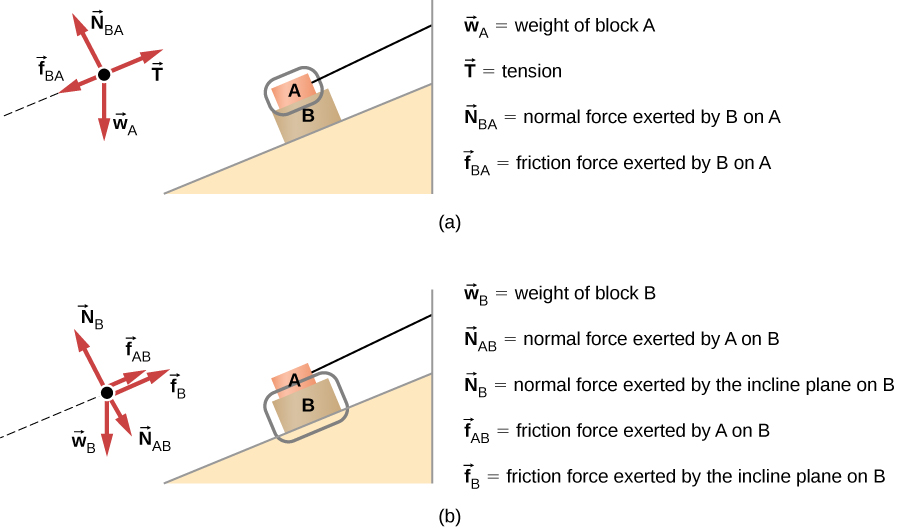
Figure v.32 (a) The free-torso diagram for isolated object A. (b) The free-trunk diagram for isolated object B. Comparing the 2 drawings, nosotros see that friction acts in the reverse direction in the two figures. Considering object A experiences a strength that tends to pull it to the right, friction must act to the left. Considering object B experiences a component of its weight that pulls information technology to the left, down the incline, the friction force must oppose information technology and human action up the ramp. Friction always acts contrary the intended direction of motion.

We now include any force that acts on the torso. Hither, no applied force is nowadays. The weight of the object acts as a strength pointing vertically downwardly, and the presence of the cord indicates a force of tension pointing away from the object. Object A has i interface and hence experiences a normal force, directed away from the interface. The source of this forcefulness is object B, and this normal force is labeled accordingly. Since object B has a tendency to slide down, object A has a tendency to slide upwardly with respect to the interface, so the friction [latex] {f}_{\text{BA}} [/latex] is directed downward parallel to the inclined plane.

As noted in stride iv of the problem-solving strategy, nosotros then construct the complimentary-body diagram in (Figure)(b) using the aforementioned arroyo. Object B experiences two normal forces and two friction forces due to the presence of two contact surfaces. The interface with the inclined plane exerts external forces of [latex] {N}_{\text{B}} [/latex] and [latex] {f}_{\text{B}} [/latex], and the interface with object B exerts the normal force [latex] {N}_{\text{AB}} [/latex] and friction [latex] {f}_{\text{AB}} [/latex]; [latex] {N}_{\text{AB}} [/latex] is directed away from object B, and [latex] {f}_{\text{AB}} [/latex] is opposing the tendency of the relative motion of object B with respect to object A.

Significance

The object nether consideration in each office of this trouble was circled in gray. When you are first learning how to draw complimentary-torso diagrams, you volition find it helpful to circle the object earlier deciding what forces are interim on that detail object. This focuses your attention, preventing you from because forces that are not acting on the body.

Example

2 Blocks in Contact

A forcefulness is applied to 2 blocks in contact, as shown.

Strategy

Draw a gratuitous-torso diagram for each block. Be sure to consider Newton's third law at the interface where the 2 blocks impact.

Solution

Significance[latex] {\overset{\to }{A}}_{21} [/latex] is the activeness forcefulness of cake two on block one. [latex] {\overset{\to }{A}}_{12} [/latex] is the reaction force of block 1 on cake 2. Nosotros use these free-body diagrams in Applications of Newton's Laws.

Instance

Cake on the Table (Coupled Blocks)

A cake rests on the table, as shown. A lite rope is attached to it and runs over a pulley. The other end of the rope is attached to a second cake. The two blocks are said to be coupled. Block [latex] {1000}_{ii} [/latex] exerts a force due to its weight, which causes the system (ii blocks and a cord) to accelerate.

Strategy

We assume that the string has no mass so that we do non have to consider information technology equally a divide object. Draw a gratis-body diagram for each block.

Solution

Significance

Each block accelerates (notice the labels shown for [latex] {\overset{\to }{a}}_{1} [/latex] and [latex] {\overset{\to }{a}}_{2} [/latex]); all the same, assuming the cord remains taut, they accelerate at the aforementioned rate. Thus, nosotros have [latex] {\overset{\to }{a}}_{one}={\overset{\to }{a}}_{2} [/latex]. If nosotros were to continue solving the problem, we could simply call the acceleration [latex] \overset{\to }{a} [/latex]. Too, nosotros use 2 free-trunk diagrams because we are usually finding tension T, which may require u.s.a. to use a system of 2 equations in this blazon of problem. The tension is the aforementioned on both [latex] {m}_{1}\,\text{and}\,{grand}_{2} [/latex].

Check Your Understanding

(a) Depict the free-torso diagram for the situation shown. (b) Redraw it showing components; use x-axes parallel to the two ramps.

Show Solution

Figure a shows a free body diagram of an object on a line that slopes downwards to the right. Pointer T from the object points right and up, parallel to the slope. Pointer N1 points left and up, perpendicular to the slope. Arrow w1 points vertically down. Arrow w1x points left and downward, parallel to the slope. Arrow w1y points correct and downwardly, perpendicular to the gradient. Figure b shows a complimentary trunk diagram of an object on a line that slopes down to the left. Arrow N2 from the object points right and up, perpendicular to the slope. Arrow T points left and up, parallel to the slope. Arrow w2 points vertically downwards. Pointer w2y points left and down, perpendicular to the slope. Pointer w2x points correct and down, parallel to the slope.

View this simulation to predict, qualitatively, how an external force will affect the speed and direction of an object's motion. Explain the furnishings with the help of a costless-body diagram. Use free-body diagrams to draw position, velocity, acceleration, and strength graphs, and vice versa. Explain how the graphs relate to one some other. Given a scenario or a graph, sketch all four graphs.

Summary

• To draw a free-trunk diagram, nosotros describe the object of involvement, draw all forces acting on that object, and resolve all force vectors into x– and y-components. We must draw a split gratuitous-body diagram for each object in the trouble.
• A gratis-body diagram is a useful ways of describing and analyzing all the forces that act on a body to make up one's mind equilibrium according to Newton's starting time law or acceleration according to Newton'southward second law.

Key Equations

Net external forcefulness	[latex] {\overset{\to }{F}}_{\text{net}}=\sum \overset{\to }{F}={\overset{\to }{F}}_{1}+{\overset{\to }{F}}_{ii}+\text{⋯} [/latex]
Newton's first law	[latex] \overset{\to }{v}=\,\text{constant when}\,{\overset{\to }{F}}_{\text{net}}=\overset{\to }{0}\,\text{N} [/latex]
Newton's second law, vector form	[latex] {\overset{\to }{F}}_{\text{net}}=\sum \overset{\to }{F}=m\overset{\to }{a} [/latex]
Newton'south second law, scalar class	[latex] {F}_{\text{net}}=ma [/latex]
Newton'due south 2d police force, component form	[latex] \sum {\overset{\to }{F}}_{x}=m{\overset{\to }{a}}_{x}\text{,}\,\sum {\overset{\to }{F}}_{y}=chiliad{\overset{\to }{a}}_{y},\,\text{and}\,\sum {\overset{\to }{F}}_{z}=m{\overset{\to }{a}}_{z}. [/latex]
Newton's second law, momentum form	[latex] {\overset{\to }{F}}_{\text{net}}=\frac{d\overset{\to }{p}}{dt} [/latex]
Definition of weight, vector form	[latex] \overset{\to }{westward}=m\overset{\to }{g} [/latex]
Definition of weight, scalar form	[latex] w=mg [/latex]
Newton's 3rd law	[latex] {\overset{\to }{F}}_{\text{AB}}=\text{−}{\overset{\to }{F}}_{\text{BA}} [/latex]
Normal force on an object resting on a horizontal surface, vector form	[latex] \overset{\to }{North}=\text{−}m\overset{\to }{1000} [/latex]
Normal force on an object resting on a horizontal surface, scalar form	[latex] N=mg [/latex]
Normal force on an object resting on an inclined airplane, scalar form	[latex] N=mg\text{cos}\,\theta [/latex]
Tension in a cablevision supporting an object of mass m at residuum, scalar form	[latex] T=w=mg [/latex]

Conceptual Questions

In completing the solution for a problem involving forces, what exercise we do later constructing the free-body diagram? That is, what do we apply?

If a book is located on a tabular array, how many forces should be shown in a gratuitous-body diagram of the book? Draw them.

Show Solution

Two forces of unlike types: weight acting downwardly and normal force acting upward

If the book in the previous question is in free fall, how many forces should be shown in a free-body diagram of the book? Describe them.

Bug

A brawl of mass chiliad hangs at residuum, suspended by a string. (a) Sketch all forces. (b) Describe the gratis-body diagram for the ball.

A car moves along a horizontal road. Draw a free-body diagram; be certain to include the friction of the road that opposes the forward motion of the car.

Show Solution

A runner pushes against the track, as shown. (a) Provide a complimentary-trunk diagram showing all the forces on the runner. (Hint: Identify all forces at the center of his trunk, and include his weight.) (b) Requite a revised diagram showing the xy-component form.

The traffic calorie-free hangs from the cables every bit shown. Draw a free-trunk diagram on a coordinate airplane for this situation.

Show Solution

Boosted Problems

Two small forces, [latex] {\overset{\to }{F}}_{1}=-2.xl\hat{i}-6.10t\hat{j} [/latex] Northward and [latex] {\overset{\to }{F}}_{2}=8.50\hat{i}-9.lxx\hat{j} [/latex] N, are exerted on a rogue asteroid by a pair of space tractors. (a) Observe the internet force. (b) What are the magnitude and direction of the internet force? (c) If the mass of the asteroid is 125 kg, what acceleration does information technology feel (in vector form)? (d) What are the magnitude and direction of the acceleration?

2 forces of 25 and 45 N human activity on an object. Their directions differ past [latex] 70\text{°} [/latex]. The resulting acceleration has magnitude of [latex] ten.0\,{\text{m/due south}}^{two}. [/latex] What is the mass of the body?

A force of 1600 Northward acts parallel to a ramp to push button a 300-kg piano into a moving van. The ramp is inclined at [latex] xx\text{°} [/latex]. (a) What is the acceleration of the piano up the ramp? (b) What is the velocity of the piano when it reaches the top if the ramp is 4.0 chiliad long and the piano starts from rest?

Draw a gratis-trunk diagram of a diver who has entered the water, moved downwards, and is acted on by an upwardly force due to the water which balances the weight (that is, the diver is suspended).

Show Solution

For a swimmer who has just jumped off a diving board, assume air resistance is negligible. The swimmer has a mass of 80.0 kg and jumps off a board 10.0 chiliad above the water. Three seconds after entering the water, her downward motion is stopped. What average upward force did the h2o exert on her?

(a) Find an equation to determine the magnitude of the internet forcefulness required to terminate a auto of mass thousand, given that the initial speed of the car is [latex] {v}_{0} [/latex] and the stopping distance is x. (b) Detect the magnitude of the internet force if the mass of the car is 1050 kg, the initial speed is 40.0 km/h, and the stopping altitude is 25.0 grand.

Show Solution

a. [latex] {F}_{\text{internet}}=\frac{thousand({v}^{2}-{v}_{0}{}^{2})}{2x} [/latex]; b. 2590 N

A sailboat has a mass of [latex] 1.50\,×\,{10}^{iii} [/latex] kg and is acted on by a force of [latex] 2.00\,×\,{10}^{3} [/latex] N toward the east, while the air current acts behind the sails with a force of [latex] 3.00\,×\,{ten}^{iii} [/latex] Northward in a direction [latex] 45\text{°} [/latex] north of east. Find the magnitude and direction of the resulting dispatch.

Find the dispatch of the body of mass ten.0 kg shown below.

Prove Answer

[latex] \begin{array}{cc} {\overset{\to }{F}}_{\text{internet}}=four.05\lid{i}+12.0\chapeau{j}\text{N}\hfill \\ {\overset{\to }{F}}_{\text{net}}=m\overset{\to }{a}⇒\overset{\to }{a}=0.405\hat{i}+ane.twenty\lid{j}\,{\text{m/due south}}^{2}\hfill \terminate{array} [/latex]

A trunk of mass two.0 kg is moving along the x-axis with a speed of three.0 1000/s at the instant represented below. (a) What is the acceleration of the trunk? (b) What is the body's velocity 10.0 s later? (c) What is its displacement afterwards 10.0 s?

Forcefulness [latex] {\overset{\to }{F}}_{\text{B}} [/latex] has twice the magnitude of forcefulness [latex] {\overset{\to }{F}}_{\text{A}}. [/latex] Notice the direction in which the particle accelerates in this effigy.

Shown below is a body of mass one.0 kg under the influence of the forces [latex] {\overset{\to }{F}}_{A} [/latex], [latex] {\overset{\to }{F}}_{B} [/latex], and [latex] grand\overset{\to }{thousand} [/latex]. If the body accelerates to the left at [latex] 20\,{\text{m/southward}}^{ii} [/latex], what are [latex] {\overset{\to }{F}}_{A} [/latex] and [latex] {\overset{\to }{F}}_{B} [/latex]?

A strength acts on a motorcar of mass m so that the speed five of the car increases with position x every bit [latex] five=k{x}^{2} [/latex], where chiliad is constant and all quantities are in SI units. Find the force acting on the automobile equally a part of position.

Show Solution

[latex] F=2kmx [/latex]; First, accept the derivative of the velocity function to obtain [latex] a=2kx [/latex]. And so apply Newton'south second police [latex] F=ma=1000(2kx)=2kmx [/latex].

A 7.0-Northward force parallel to an incline is applied to a 1.0-kg crate. The ramp is tilted at [latex] 20\text{°} [/latex] and is frictionless. (a) What is the acceleration of the crate? (b) If all other weather are the same but the ramp has a friction force of 1.9 N, what is the acceleration?

Two boxes, A and B, are at rest. Box A is on level ground, while box B rests on an inclined plane tilted at bending [latex] \theta [/latex] with the horizontal. (a) Write expressions for the normal force interim on each block. (b) Compare the ii forces; that is, tell which one is larger or whether they are equal in magnitude. (c) If the angle of incline is [latex] ten\text{°} [/latex], which strength is greater?

Bear witness Solution

a. For box A, [latex] {N}_{\text{A}}=mg [/latex] and [latex] {Due north}_{\text{B}}=mg\,\text{cos}\,\theta [/latex]; b. [latex] {N}_{\text{A}}>{N}_{\text{B}} [/latex] considering for [latex] \theta <ninety\text{°} [/latex], [latex] \text{cos}\,\theta <1 [/latex]; c. [latex] {N}_{\text{A}}>{N}_{\text{B}} [/latex] when [latex] \theta =10\text{°} [/latex]

A mass of 250.0 m is suspended from a spring hanging vertically. The bound stretches 6.00 cm. How much will the leap stretch if the suspended mass is 530.0 grand?

As shown below, two identical springs, each with the jump constant 20 Due north/thousand, support a xv.0-N weight. (a) What is the tension in spring A? (b) What is the amount of stretch of spring A from the residue position?

Bear witness Solution

a. viii.66 N; b. 0.433 m

Shown below is a 30.0-kg block resting on a frictionless ramp inclined at [latex] sixty\text{°} [/latex] to the horizontal. The cake is held past a spring that is stretched 5.0 cm. What is the strength abiding of the leap?

In building a house, carpenters utilise nails from a large box. The box is suspended from a spring twice during the day to measure out the usage of nails. At the offset of the mean solar day, the bound stretches 50 cm. At the end of the 24-hour interval, the leap stretches 30 cm. What fraction or percentage of the nails have been used?

Show Solution

0.40 or forty%

A force is applied to a block to motion it up a [latex] 30\text{°} [/latex] incline. The incline is frictionless. If [latex] F=65.0\,\text{N} [/latex] and [latex] M=five.00\,\text{kg} [/latex], what is the magnitude of the acceleration of the block?

2 forces are applied to a 5.0-kg object, and it accelerates at a rate of [latex] 2.0\,{\text{m/s}}^{two} [/latex] in the positive y-direction. If 1 of the forces acts in the positive x-direction with magnitude 12.0 N, detect the magnitude of the other force.

The block on the right shown below has more mass than the block on the left ([latex] {m}_{2}>{m}_{i} [/latex]). Depict free-body diagrams for each cake.

Claiming Bug

If ii tugboats pull on a disabled vessel, as shown here in an overhead view, the disabled vessel will exist pulled along the direction indicated by the result of the exerted forces. (a) Describe a costless-body diagram for the vessel. Assume no friction or elevate forces impact the vessel. (b) Did you include all forces in the overhead view in your free-body diagram? Why or why non?

A ten.0-kg object is initially moving east at fifteen.0 m/s. Then a force acts on information technology for 2.00 due south, afterward which it moves northwest, besides at 15.0 grand/s. What are the magnitude and direction of the average force that acted on the object over the 2.00-s interval?

On June 25, 1983, shot-putter Udo Beyer of East Deutschland threw the 7.26-kg shot 22.22 one thousand, which at that time was a earth record. (a) If the shot was released at a height of ii.twenty one thousand with a projection angle of [latex] 45.0\text{°} [/latex], what was its initial velocity? (b) If while in Beyer'south hand the shot was accelerated uniformly over a distance of 1.20 m, what was the net force on it?

Testify Solution

a. 14.i one thousand/due south; b. 601 North

A body of mass thou moves in a horizontal direction such that at time t its position is given by [latex] x(t)=a{t}^{4}+b{t}^{3}+ct, [/latex] where a, b, and c are constants. (a) What is the acceleration of the trunk? (b) What is the time-dependent force acting on the torso?

A trunk of mass m has initial velocity [latex] {v}_{0} [/latex] in the positive 10-direction. It is acted on by a abiding strength F for time t until the velocity becomes zero; the force continues to act on the body until its velocity becomes [latex] \text{−}{v}_{0} [/latex] in the aforementioned amount of fourth dimension. Write an expression for the full distance the body travels in terms of the variables indicated.

Show Solution

[latex] \frac{F}{m}{t}^{2} [/latex]

The velocities of a 3.0-kg object at [latex] t=6.0\,\text{southward} [/latex] and [latex] t=8.0\,\text{south} [/latex] are [latex] (iii.0\chapeau{i}-six.0\lid{j}+4.0\lid{k})\,\text{m/s} [/latex] and [latex] (-ii.0\lid{i}+iv.0\hat{k})\,\text{m/south} [/latex], respectively. If the object is moving at constant acceleration, what is the force acting on it?

A 120-kg astronaut is riding in a rocket sled that is sliding forth an inclined plane. The sled has a horizontal component of acceleration of [latex] 5.0\,\text{m}\text{/}{\text{south}}^{two} [/latex] and a downward component of [latex] 3.viii\,\text{1000}\text{/}{\text{s}}^{ii} [/latex]. Calculate the magnitude of the forcefulness on the rider by the sled. (Hint: Think that gravitational acceleration must exist considered.)

Two forces are interim on a 5.0-kg object that moves with acceleration [latex] 2.0\,{\text{m/s}}^{2} [/latex] in the positive y-management. If one of the forces acts in the positive 10-direction and has magnitude of 12 N, what is the magnitude of the other force?

Suppose that yous are viewing a soccer game from a helicopter above the playing field. Ii soccer players simultaneously boot a stationary soccer ball on the flat field; the soccer ball has mass 0.420 kg. The showtime role player kicks with force 162 N at [latex] 9.0\text{°} [/latex] north of west. At the same instant, the 2d player kicks with force 215 N at [latex] fifteen\text{°} [/latex] eastward of due south. Find the acceleration of the ball in [latex] \hat{i} [/latex] and [latex] \chapeau{j} [/latex] form.

Prove Solution

[latex] [/latex][latex] \overset{\to }{a}=-248\hat{i}-433\hat{j}\text{m}\text{/}{\text{s}}^{two} [/latex]

A 10.0-kg mass hangs from a spring that has the jump constant 535 N/grand. Notice the position of the stop of the spring away from its rest position. (Apply [latex] g=ix.fourscore\,{\text{thou/s}}^{2} [/latex].)

A 0.0502-kg pair of fuzzy dice is attached to the rearview mirror of a car by a short cord. The automobile accelerates at abiding charge per unit, and the die hang at an angle of [latex] iii.twenty\text{°} [/latex] from the vertical because of the car's acceleration. What is the magnitude of the dispatch of the car?

Show Solution

[latex] 0.548\,{\text{1000/due south}}^{ii} [/latex]

At a circus, a ass pulls on a sled carrying a modest clown with a force given by [latex] 2.48\hat{i}+4.33\chapeau{j}\,\text{N} [/latex]. A horse pulls on the aforementioned sled, aiding the hapless donkey, with a force of [latex] 6.56\hat{i}+5.33\chapeau{j}\,\text{N} [/latex]. The mass of the sled is 575 kg. Using [latex] \lid{i} [/latex] and [latex] \chapeau{j} [/latex] form for the answer to each problem, find (a) the net strength on the sled when the two animals act together, (b) the acceleration of the sled, and (c) the velocity after half dozen.50 s.

Hanging from the ceiling over a baby bed, well out of baby's reach, is a string with plastic shapes, as shown here. The string is taut (there is no slack), as shown past the straight segments. Each plastic shape has the same mass m, and they are as spaced past a distance d, as shown. The angles labeled [latex] \theta [/latex] draw the angle formed past the end of the string and the ceiling at each end. The center length of sting is horizontal. The remaining two segments each course an angle with the horizontal, labeled [latex] \varphi [/latex]. Let [latex] {T}_{1} [/latex] exist the tension in the leftmost section of the string, [latex] {T}_{ii} [/latex] exist the tension in the section adjacent to it, and [latex] {T}_{3} [/latex] be the tension in the horizontal segment. (a) Detect an equation for the tension in each section of the string in terms of the variables one thousand, g, and [latex] \theta [/latex]. (b) Find the angle [latex] \varphi [/latex] in terms of the angle [latex] \theta [/latex]. (c) If [latex] \theta =5.10\text{°} [/latex], what is the value of [latex] \varphi [/latex]? (d) Find the distance ten between the endpoints in terms of d and [latex] \theta [/latex].

Bear witness Solution

a. [latex] {T}_{ane}=\frac{2mg}{\text{sin}\,\theta } [/latex], [latex] {T}_{2}=\frac{mg}{\text{sin}(\text{arctan}(\frac{one}{2}\text{tan}\,\theta ))} [/latex], [latex] {T}_{3}=\frac{2mg}{\text{tan}\,\theta }; [/latex] b. [latex] \varphi =\text{arctan}(\frac{1}{2}\text{tan}\,\theta ) [/latex]; c. [latex] 2.56\text{°} [/latex]; (d) [latex] x=d(2\,\text{cos}\,\theta +2\,\text{cos}(\text{arctan}(\frac{one}{2}\text{tan}\,\theta ))+1) [/latex]

A bullet shot from a burglarize has mass of ten.0 g and travels to the right at 350 m/s. It strikes a target, a large bag of sand, penetrating it a altitude of 34.0 cm. Find the magnitude and direction of the retarding force that slows and stops the bullet.

An object is acted on by three simultaneous forces: [latex] {\overset{\to }{F}}_{1}=(-iii.00\hat{i}+2.00\hat{j})\,\text{N} [/latex], [latex] {\overset{\to }{F}}_{2}=(6.00\hat{i}-4.00\lid{j})\,\text{N} [/latex], and [latex] {\overset{\to }{F}}_{iii}=(2.00\hat{i}+5.00\chapeau{j})\,\text{N} [/latex]. The object experiences acceleration of [latex] 4.23\,{\text{thou/due south}}^{2} [/latex]. (a) Detect the acceleration vector in terms of chiliad. (b) Find the mass of the object. (c) If the object begins from residue, detect its speed afterward 5.00 s. (d) Discover the components of the velocity of the object subsequently five.00 s.

Show Solution

a. [latex] \overset{\to }{a}=(\frac{5.00}{m}\hat{i}+\frac{3.00}{k}\hat{j})\,\text{m}\text{/}{\text{south}}^{2}; [/latex] b. 1.38 kg; c. 21.two yard/due south; d. [latex] \overset{\to }{v}=(18.i\lid{i}+10.nine\hat{j})\,\text{m}\text{/}{\text{due south}}^{2} [/latex]

In a particle accelerator, a proton has mass [latex] 1.67\,×\,{x}^{-27}\,\text{kg} [/latex] and an initial speed of [latex] 2.00\,×\,{10}^{5}\,\text{m}\text{/}\text{s.} [/latex] It moves in a straight line, and its speed increases to [latex] 9.00\,×\,{10}^{v}\,\text{grand}\text{/}\text{s} [/latex] in a distance of 10.0 cm. Presume that the dispatch is constant. Find the magnitude of the strength exerted on the proton.

A drone is existence directed beyond a frictionless ice-covered lake. The mass of the drone is i.50 kg, and its velocity is [latex] three.00\chapeau{i}\text{one thousand}\text{/}\text{southward} [/latex]. After 10.0 s, the velocity is [latex] 9.00\hat{i}+four.00\hat{j}\text{thousand}\text{/}\text{south} [/latex]. If a constant strength in the horizontal direction is causing this change in motion, discover (a) the components of the force and (b) the magnitude of the strength.

Show Solution

a. [latex] 0.900\chapeau{i}+0.600\chapeau{j}\,\text{N} [/latex]; b. 1.08 Due north

Source: https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/5-7-drawing-free-body-diagrams/

Posted by: sullivanwouniend1968.blogspot.com

Share this post